Beautiful Aggregations with Haskell
by @eborden on September 22, 2017
Aggregating data is a common, tedious task. In imperative languages we often end up with a rat’s nest of mutable variables, nested loops and other awful constructs. In functional languages a naive implementation also results in spaghetti and usually less than ideal performance. We can do better. We can build fast, declarative, easy to understand and easy to maintain aggregations in Haskell.
What is an Aggregate?
One of the simplest definitions of an aggregate is:
A whole formed by combining several separate elements.
Postgres defines an aggregate as:
A single result from a set of input values.
Aggregates in Haskell
Haskell has many aggregate functions min and max, sum, length, etc. These
all live in base and provide great utility. However, once we start combining
aggregates their utility falls apart. A common example is computing an average:
average :: [Float] -> Float
average xs = sum xs / fromIntegral (length xs)
This works, but it is wasteful. It has to force evaluation of xs to compute sum.
Then it calculates length. Finally doing division. This means our entire list
will be in memory and we need to loop over it twice. This is bad and can destroy
performance. We’d rather utilize one loop, while only keeping as much data in
memory as necessary.
A Better Way
In Haskell, whenever we find ourselves combining (or crushing) many elements
into one we reach for Semigroup
and Monoid, often paired with
Foldable.
foldMap :: (Foldable t, Monoid m) => (a -> m) -> t a -> m
or its Semigroup counterpart
foldMap1 :: (Foldable1 t, Semigroup s) => (a -> s) -> t a -> s
These building blocks can allow us to create principled, readable and performant aggregations.
Postgres Aggregates in Haskell
How would we represent common Postgres aggregations in Haskell?
For many aggregations Data.Monoid and Data.Semigroup already have you
covered.
sum
import Data.Monoid (Sum)
getSum $ foldMap Sum [2, 4, 1, 3]
> 10
count
import Data.Monoid (Sum)
getSum $ foldMap (const $ Sum 1) [2, 4, 1, 3]
> 4
bool_and
import Data.Semigroup (All)
getAll $ foldMap All [True, True, True]
> True
getAll $ foldMap All [True, False, True]
> False
bool_or
import Data.Semigroup (Any)
getAny $ foldMap Any [True, False, True]
> True
getAny $ foldMap Any [False, False, False]
> False
max
import Data.Semigroup (Max)
getMax . foldMap1 Max $ NonEmpty.fromList [1, 4, 2, 3]
> 4
min
import Data.Semigroup (Min)
getMin . foldMap1 Min $ NonEmpty.fromList [2, 4, 1, 3]
> 1
What is in a Sum?
If we look deeper into Sum we can see how simple many Monoids are:
newtype Sum a = Sum { getSum :: a }
instance Num a => Monoid (Sum a) where
mempty = Sum 0
mappend (Sum x) (Sum y) = Sum $ x + y
Wrapping addition in all this type machinery seems silly. Soon we’ll see that this allows powerful and principled composition.
What About Average?
A canonical package for an Average monoid doesn’t currently exist.
Our naive average is (sum xs / length xs). We can break this into a fast
canonical form by decomposing its elements into accumulators:
data Average n = Average { length :: !Int, sum :: !n }
averageDatum :: n -> Average n
averageDatum n = Average 1 n
getAverage :: (Num n, Fractional n) => Average n -> Maybe n
getAverage (Average l n) =
if l == 0
then Nothing
else Just $ n / fromIntegral l
instance Num n => Semigroup (Average n) where
Average lx nx <> Average ly ny = Average (lx + ly) (nx + ny)
instance Num n => Monoid (Average n) where
mappend = (<>)
mempty = Average 0 0
This Average data type encapsulates length and summation while allowing us to
calculate these values in one pass. Decomposing formulas into accumulators is
used pervasively in streaming abstractions and this Average type shows up time
and time again.
getAverage $ foldMap averageDatum [1, 2, 3, 4, 5]
> Just 3
How About Group By?
When we aggregate we often do so in association with or grouped by another piece
of data. “I want the maximum price paid for each item on ebay.” We group data
with Data.Map or Data.HashMap, but there is one hitch.
The Monoid and Semigroup instances of these data types are left biased:
foldMap (uncurry HashMap.singleton . second Sum) [(1, 2), (1, 3), (1, 4)]
> fromList [(1, Sum 2)]
We want a Monoid instance that mappends our data!
Like any good haskeller we turn to the hammer of newtypeing to get the
instance we want. We can wrap HashMap or Map
newtype MergeMap k v = MergeMap {getMergeMap :: HashMap k v}
instance (Monoid v, Eq k, Hashable k) => Monoid (MergeMap k v) where
mempty = MergeMap HashMap.empty
MergeMap x `mappend` MergeMap y = MergeMap $ HashMap.unionWith mappend x y
Now we can happily foldMap our grouped data without worry.
getMergeMap $ foldMap (MergeMap . uncurry HashMap.singleton . second Sum) [(1, 2), (1, 3), (1, 4)]
> fromList [(1, Sum 9)]
If you are a proponent of Semigroup then you might say, “Hey! Every Monoid is
a Semigroup. Where’s my instance?” And you’d be right. We can build a
Semigroup instance like so:
instance (Semigroup v, Eq k, Hashable k) => Semigroup (MergeMap k v) where
MergeMap x <> MergeMap y = MergeMap $ HashMap.unionWith (<>) x y
This also reveals an important principle. Our Monoid instance is overly
restrictive. We can weaken the param to Semigroup and our wrapped HashMap
will do the work of providing mempty for us.
instance (Semigroup v, Eq k, Hashable k) => Monoid (MergeMap k v) where
mempty = MergeMap mempty -- mempty from (HashMap k v)
mappend = (<>)
There are technical reasons for why this is true, but a simple way to think of
it is any parameterized Monoid can legally contain a Semigroup if its
mempty instance does not require calling mempty on its type param. The Maybe
type is one of the simplest forms of this. Compare Maybe a with Either l r.
data Maybe a = Nothing | Just a
instance Semigroup a => Monoid (Maybe a) where
mempty = Nothing
mappend = _
data Either l r = Left l | Right r
instance Monoid r => Monoid (Either l r) where
mempty = Right mempty -- crap we need mempty for r
mappend = _
We don’t need the type parameter to produce a Nothing value *, but
we do need the type param for Right to produce a mempty.
This has very practical implications. It means we can calculate Semigroup
values like Min and Max from empty lists as long as we wrap them in an
appropriate Monoid:
foldMap (Just . Max) [2, 3, 4]
> Just (Max 4)
getMergeMap $ foldMap (MergeMap . uncurry HashMap.singleton . second Min) [(1, 2), (1, 3), (1, 4)]
> fromList [(1, Min 2)]
Building Complex Aggregates
So we can aggregate single values, but what about aggregating many values at once? What about a query like this:
select pet_type, min(num_legs), max(num_legs) from pets group by pet_type;
First we need to aggregate min and max. We could do this in two passes.
let inTwo = (min, max)
where
min = fmap getMin $ foldMap (Just . Min) [1, 2, 3, 4]
max = fmap getMax $ foldMap (Just . Max) [1, 2, 3, 4]
> (Just 1, Just 4)
But that is two passes. We can do better by leveraging the Monoid instance
of our tuple, (,).
minMax x = (Just $ Min x, Just $ Max x)
getMinMax = bimap (fmap getMin) (fmap getMax)
inOne = getMinMax $ foldMap minMax [1, 2, 3, 4]
> (Just 1, Just 4)
Now lets pull it all together with our grouping:
petData = [("dog", 3), ("turkey", 2), ("turkey", 2), ("dog", 4)]
fmap getMinMax . getMergeMap
$ foldMap (MergeMap . uncurry HashMap.singleton . second minMax) petData
> fromList [("dog", (3, 4)), ("turkey", (2, 2))]
Awesome, we were able to group and compute Min and Max in a single loop.
Custom Data Types
As our aggregates grow in complexity we likely want to avoid tuples. They are
great for small bits of data, but their laziness properties aren’t ideal for
smashing data together and long tuples become hard to read or even ambiguous.
We want to create custom data types:
data PetAggregate
= PetAggregate
{ minNumberOfLegs :: !(Min Natural)
, maxNumberOfLegs :: !(Max Natural)
, numCanSwim :: !(Sum Natural)
, averageWeight :: !(Average Double)
}
instance Semigroup PetAggregate where
(<>) x y
= PetAggregate
{ minNumberOfLegs = on (<>) minNumberOfLegs x y
, maxNumberOfLegs = on (<>) maxNumberOfLegs x y
, numCanSwim = on (<>) numCanSwim x y
, averageWeight = on (<>) averageWeight x y
}
So What?
Okay, so we can aggregate information, who cares? We can do this in Postgres, likely faster, while our data and computation is co-located on the database. Why pull data back to our client to do this work?
One prime example is calculating multiple granularities of the same data. Take the following table:
CREATE TABLE answers
( student_grade integer NOT NULL
, teacher_name text NOT NULL
, accuracy real NOT NULL
);
We want to know:
- The average, min and max accuracy across all answers.
- The average, min and max accuracy by grade.
- The average, min and max accuracy by teacher.
With a single query Postgres will only allow us to group at the finest granularity.
SELECT avg(accuracy), min(accuracy), max(accuracy), student_grade, teacher_name
FROM answer
GROUP BY student_grade, teacher_name;
We can likely do some SQL wizardry, but what complexity cost are we buying? We could make multiple calls to the DB, but then we are writing more SQL and de-serializing the same data for every granularity.
Instead we can use Postgres for fine grain aggregation and use our new monoidal super powers to do the rest.
First we define a data type that encompasses our simple answer aggregations.
data AnswerAgg
= AnswerAgg
{ averageAccuracy :: !(Average Double)
, minAccuracy :: !(Min Double)
, maxAccuracy :: !(Max Double)
}
instance Semigroup AnswerAgg where
x <> y =
AnswerAgg
{ averageAccuracy = on (<>) averageAccuracy x y
, minAccuracy = on (<>) minAccuracy x y
, maxAccuracy = on (<>) maxAccuracy x y
}
Then we define a data type that pulls those all together, grouping some with
MergeMap.
data MultiGranularityAgg
= MultiGranularityAgg
{ globalAgg :: Option AnswerAgg
, byGrade :: MergeMap Natural AnswerAgg
, byTeacher :: MergeMap Text AnswerAgg
}
instance Semigroup MultiGranularityAgg where
x <> y =
MultiGranularityAgg
{ globalAgg = on (<>) globalAgg x y
, byGrade = on (<>) byGrade x y
, byTeacher = on (<>) byTeacher x y
}
instance Monoid MultiGranularityAgg where
mappend = (<>)
mempty = MultiGranularityAgg mempty mempty mempty
Then we write a function that converts a single row of data into our aggregation type, nesting and all.
singletonAggregate
:: (Int, Double, Double, Double, Natural, Text)
-> MultiGranularityAgg
singletonAggregate (numAnswer, sumAccuracy, minAccuracy, maxAccuracy, grade, teacherName) =
MultiGranularityAgg
{ globalAgg = Option $ Just answerAgg
, byGrade = MergeMap $ HashMap.singleton grade answerAgg
, byTeacher = MergeMap $ HashMap.singleton teacherName answerAgg
}
where
answerAgg =
AnswerAgg
{ averageAccuracy = Average numAnswer sumAccuracy
, minAccuracy = Min minAccuracy
, maxAccuracy = Max maxAccuracy
}
At last we glue it all together with our friend foldMap.
fetchAggregate = do
rawData <- fetchRawData
pure $ foldMap singletonAggregate rawData
Finally! With one database query, a single pass over the data and exceptional declarative style, we have a method for building complex grouped aggregates. Even better this continues to scale as we add other groupings, evening nesting groupings inside of other groupings.
Further
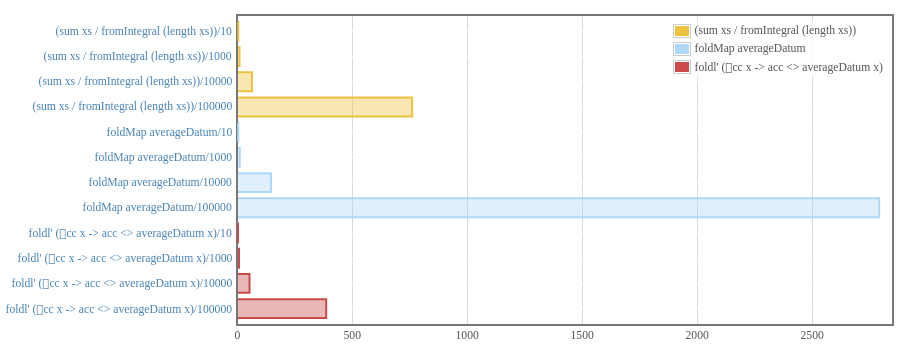
Strictly Speaking
foldMap is often implemented as a lazy right fold. That means we are not
squeezing out every last ounce of performance. Instead we could use a left fold,
which is only a bit more awkward.
foldl' (\acc x -> acc <> singletonAggregate x) mempty rawData
With this we can truly start seeing high performing folds.
Are We Streaming Yet?
This method also scales to your favorite streaming abstraction. Run your aggregations streaming and in constant memory with:
-
Conduit:
C.foldMap singletonAggregate -
Foldl:
L.foldMap singletonAggregate -
Pipes:
P.each xs >-> P.map singletonAggregate & P.fold (flip (<>)) mempty id -
Streaming:
S.fold (flip (<>)) mempty . S.map singletonAggregate
Advanced Aggregates
There are many aggregations that do not have easy streaming, Semigroup or Monoidal
algorithms, such as a median. This is an active area of research with many interesting
results. One great option is TDigest.
TDigest can estimate quantiles, histograms, medians, variance, standard deviation
and more. It also has a Semigroup instance that is not technically law abiding, but
is “morally correct”.
Prior Art
Notes
* Unfortunately Semigroup has only recently made it into base, so
the current Monoid instance of
Maybe
is overly restrictive. The
Option
newtype from Data.Semigroup allows us to override this and get the instance
we want.